概括
DeepFM模型是华为诺亚实验室于2017年发布的推荐系统模型(论文链接)。这篇文章是基于Google的Wide & Deep模型的改进和提升,被广泛的应用在工程推荐系统上。
DeepFM是基于Wide & Deep模型思想的,因此模型的结构也是同样用一个浅层模型来提取记忆,即出现过的特征组合,一个深层模型负责泛化,即搜索新的特征组合。DeepFM对于Wide & Deep的改进主要有:
- Wide模型由LR修改成了FM(Factor Machine),FM可以起到自动学习交叉特征的作用,避免了外积交叉特征工程部分。
- 共享原始输入特征,原始的特征即用在Wide模型,又用在Deep模型上,也是为了简化特征工程。
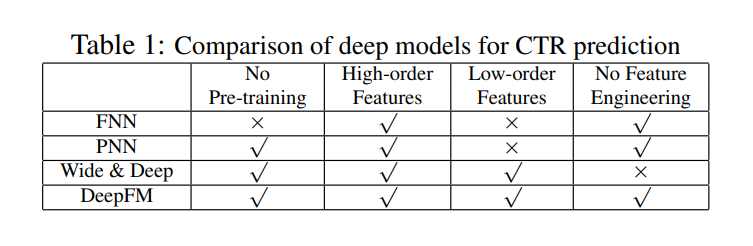
DeepFM和其他推荐系统模型比较:
模型结构
DeepFM分为FM和DNN两部分,就像前面讨论的,这两部分共享相同的输入权重 。对于一个简单一阶特征$i$, 用一个标量 $\omega_{i}$来描述特征权重,同时引入一个隐向量$V_{i}$ 来描述这个特征和其他特征之间的交互性影响,并构造FM模型以期待模型自动学习出这个特征的隐向量表达$V_{i}$.
模型的训练过程类似Wide & Deep, Wide模型和Deep模型联合训练,联合训练的模型的表达式:
\[\hat{y} = sigmoid(y_{FM} + y_{DNN})\]-
FM模型
FM模型的结构如图所示。相比于Wide & Deep的特征外积只能在连两个特征同时显性出现,FM这种隐向量表达的方法更适用于挖掘更深层次的特征耦合。
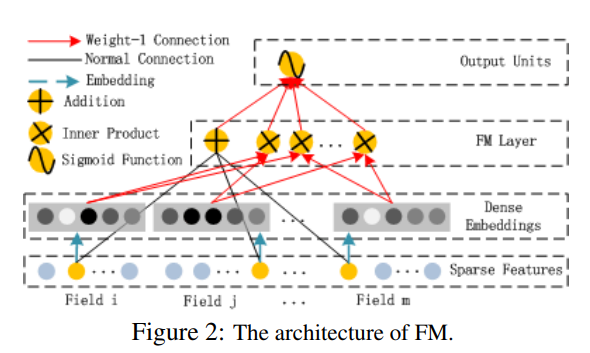
FM部分的输出表达式写作:
\[y_{FM} = <\omega, x> + \sum_{j_1=1}^{d}\sum_{j_2=j_1+1}^{d}<V_{i}, V_{j}>x_{j_1} \cdot x_{j_2}\]FM模型里面的一些参数还是要着重理解一下的,原文中对FM层的Embedding结构也做了详细的说明,这里我的理解公式在记号上可能有一些小小的偏差,公式里面的$i, j$代表的是不同的field,而公式最后的feature value的下标,应该对应的是field $i$ 和 field $j$.
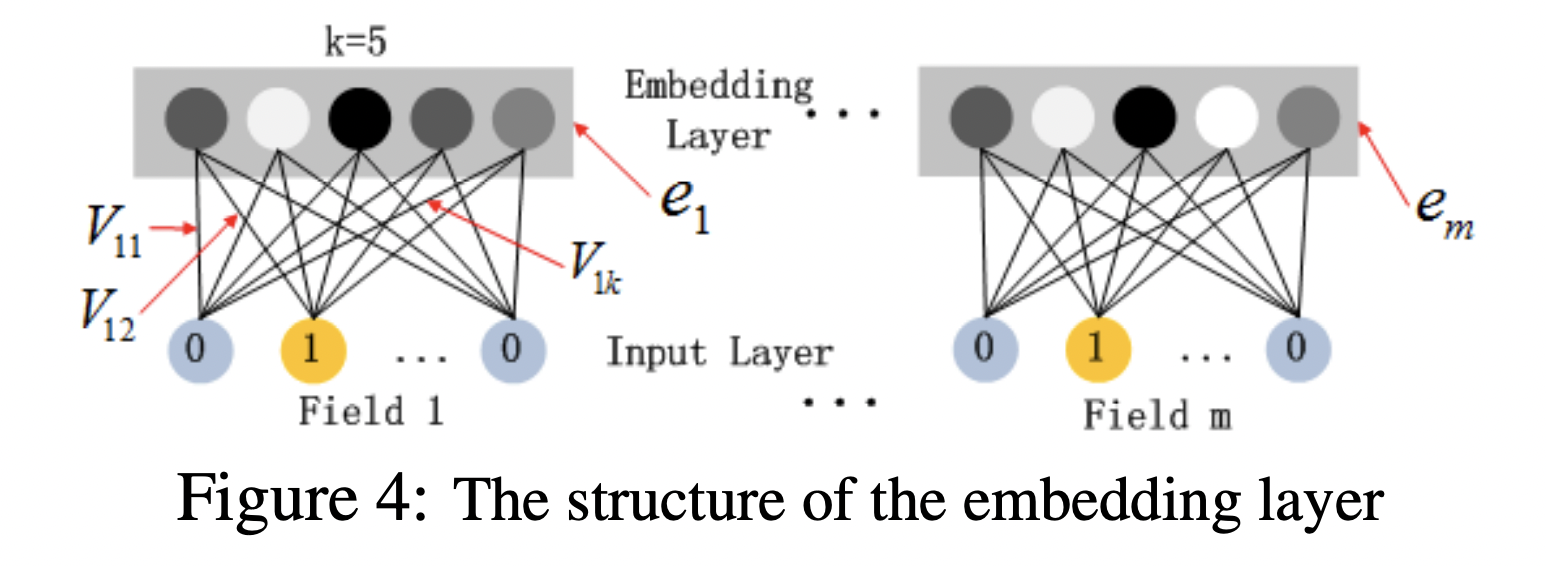
上图是原文里面对Embedding层的解释,这里我再补充一张图。共有$m$个field, 每个field对应一个one-hot向量,每个field的输入长度可以不同, 成为一个sparse feature. Embedding层的每个圆点代表一个神经元,神经元本身是没有数值的,sparse feature到Embedding神经元的连线权重,就是所谓的Embedding Vector $V$. 图上所示一共有$m$个field,每个field对应着$k$个嵌入维度,$m$个field对应的总特征维度和为$N$, 所以总的嵌入层的权重个数为$N \times k$. 第$i$个field的one-hot向量作用在第$j$个Embedding神经元上面的权重记作$V_{ij}$,像上面的原文示意图里面,第一个field的one-ho向量分别作用在5个Embedding神经元上面,权重分别是$V_{11},V_{12},V_{13},V_{14},V_{15}$,这5个值组合起来就是上面FM公式中所提到的$V_{1}$,在FM部分和DNN部分,这个Embedding的$V$向量是共享权重的,对于同一特征来说,得到的$V_{i}$是相同的。

二维特征的推导参考这篇博客:
\[\begin{aligned} \sum_{i=1}^{n-1}\sum_{j=i+1}^{n}<V_{i}, V_{j}>x_{i}x_{j} & = \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}<V_{i}, V_{j}>x_{i}x_{j} - \frac{1}{2}\sum_{i=1}^{n}<V_{i}, V_{i}>x_{i}x_{i} \\ &= \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\sum_{f=1}^{K}(v_{i, f} * v_{j, f})x_{i}x_{j} - \frac{1}{2} \sum_{i=1}^{n}\sum_{f=1}^{K}(v_{i, f} * v_{i, f})x_{i}x_{i} \\ &= \frac{1}{2}\sum_{f=1}^{K}\left((\sum_{i=1}^{n}(v_{i, f} * x_{i})(\sum_{j=1}^{n}(v_{j, f} * x_{j})) - \frac{1}{2}\sum_{i=1}^{n}(v_{i, f} * x_{i})^{2}\right) \\ &= \frac{1}{2}\sum_{f=1}^{K}\left((\sum_{i=1}^{n} v_{i, f} * x_{i})^{2} - \sum_{i=1}^{n}(v_{i, f} * x_{i})^{2}\right) \end{aligned}\] -
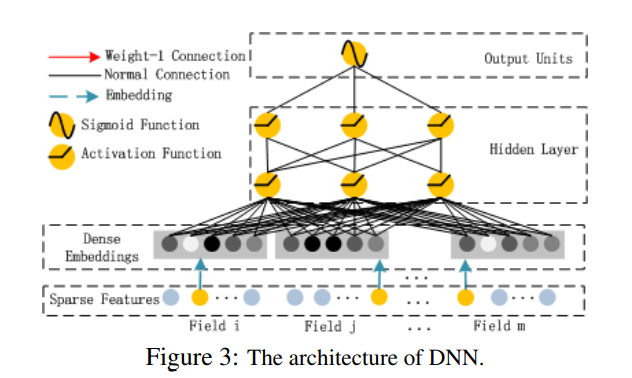
DNN模型
DNN模型的结构如图所示。CTR模型的输入向量大部分都是非常稀疏的,因此必须引入Embeddeding层。DeepFM的Embedding层的设计有下面的特点:(1)输入维度可以不同,输出维度必须相同;(2)FM模型中,特征$i$的隐向量$V_{i}$被复用到DNN模型作为特征压缩的权重。这一点很重要,也是DeepFM模型的精髓,FM部分的权重是通过FM和DNN模型整体训练出来的,而不是单独用FM模型训练再利用的。
一些总结
DeepFM从推出后在工业界的得到了广泛的应用,其先进的思想主要是用FM模型来替代Wide & Deep模型中的Wide部分。而FM训练的隐向量,刚好又被用来作为Deep模型里面的特征表达向量,从而避免了复杂的特征工程,真正实现了end-to-end的推荐系统。